T&T Zichtbaarheid berekening
Fouten bij het werpen van de vlieg naar zichtbare vis
B.Veldmeijer
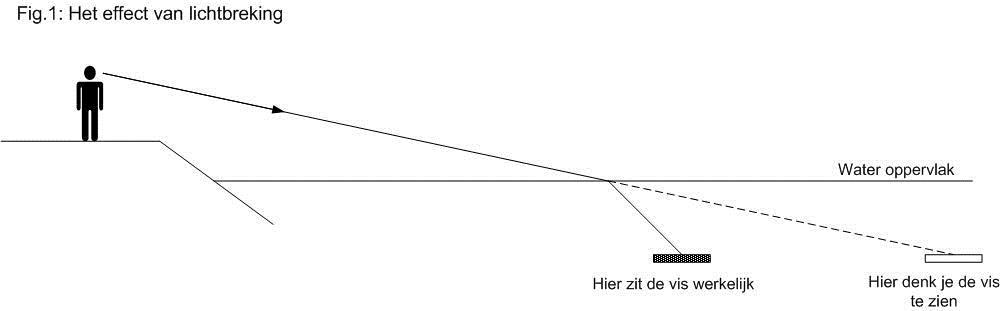
Als je in helder water duidelijk vissen kunt zien zwemmen is de kans groot dat zij bij het plaatsen van de vlieg worden verjaagd. De oorzaak is dan meestal het zogenaamde “overwerpen”. Hierbij ziet de vis de vliegenlijn over zich heen scheren en is meteen vertrokken.
Overwerpen vindt plaats als geen rekening wordt gehouden met de lichtbreking aan het wateroppervlak. Door deze lichtbreking (refractie) lijkt de vis verder weg dan hij in werkelijkheid is. Een en ander is weergegeven in fig.1.
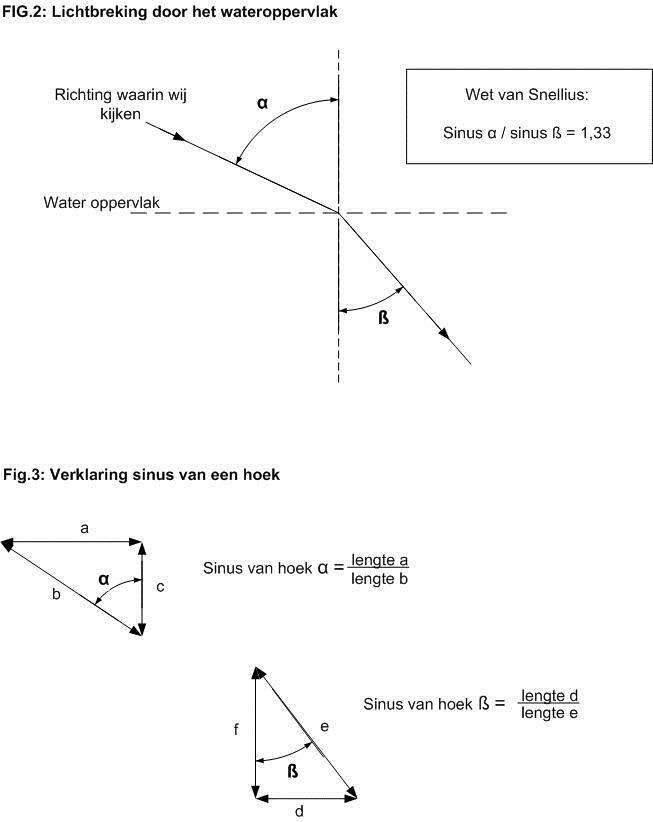
De breking van licht aan het wateroppervlak is ooit onderzocht door Snellius. Hij ontdekte dat de breking van het licht kon worden beschreven door de formule zoals gegeven in fig. 2 en 3.
De waarde 1,33 wordt ook wel aangeduid als de “ brekingsindex van water”.
Het is voor de vliegvisser dus van belang om iets meer te weten van lichtbreking als hij werpt naar zichtbare vis. De vraag is dan:
Op welke afstand zwemt de vis werkelijk en hoe voorkom ik overwerpen?
In feite wordt overwerpen voorkomen door de worp korter te maken dan je in eerste instantie inschat op basis van jouw waarneming van de vis. Aan de hand van berekende waarden in tabel 1 worden hier enkele tips gegeven om overwerpen te voorkomen. De methode voor berekening van de waarden in tabel 1 is gegeven op bladzijde 3: “ Voorbeeld voor berekening van de werkelijke afstand tot de vis”. De rekenliefhebber kan daarmee iedere situatie doorrekenen.
Tabel 1: Resultaten van berekening van de werkelijke afstand waarop de vis zich bevindt.
| Rekenvoorbeeld |
1 |
2 |
3 |
4 |
| Diepte waarop de vis zich bevindt |
0,5 m |
0,5 m |
0,5 m |
0,2 m |
| Ooghoogte boven wateroppervlak |
2 m |
1 m |
2 m |
2 m |
| Schijnbare afstand tot de vis |
10 m |
10 m |
8 m |
10 m |
| Werkelijke afstand tot de vis |
8,6 m |
7,6 m |
8,5 m |
9,4 m |
|
Overschatting van de afstand |
1,4 m |
2,4 m |
1,5 m |
0,6 m |
De waarden in tabel 1 zijn in de praktijk natuurlijk niet nauwkeurig vast te stellen. De (schijnbare) afstand tot de vis en de diepte waarop hij zich bevindt zijn slechts bij benadering te bepalen door de visser. Zelfs met een ruwe schatting kan een visser aardig uit de voeten met het verschijnsel “lichtbreking”. Dit wordt duidelijk als je de volgende conclusies op basis van tabel 1 bekijkt:
- Als de vis hoog aan het oppervlak zwemt speelt de lichtbreking nauwelijks een rol en is de kans op overwerpen gering. Juist als de vis dieper zwemt moet de lengte van de worp korter zijn dan de geschatte afstand. Vergelijk hiervoor rekenvoorbeelden 4 en 1: Als de vis op 20 cm diepte zwemt is de overschatting van de werkelijke afstand beduidend minder dan wanneer hij op 50 cm diepte zwemt.
- Als de visser knielt tijdens het werpen of als hij een lage standplaats zoekt is hij weliswaar minder zichtbaar voor de vis, maar de kans op overwerpen wordt dan beduidend groter. Vergelijk hiervoor rekenvoorbeelden 1 en 2, waarbij de ooghoogte respectievelijk 2 en 1 meter bedraagt.
- Als de schijnbare afstand tot de vis verkeerd wordt geschat heeft dit slechts weinig effect op de kans tot overwerpen. Vergelijk hiervoor rekenvoorbeelden 1 en 3. Bij een schijnbare afstand van 10 of 8 meter is de overschatting van de werkelijke afstand vrijwel gelijk.
Hoe ga je nu in de praktijk te werk?
Uit de rekenvoorbeelden in tabel 1 is de volgende vuistregel af te leiden:
Werp een leaderlengte korter dan je denkt nodig te hebben. Reageert de vis niet, dan moet je de worpen telkens met ongeveer één meter verlengen.
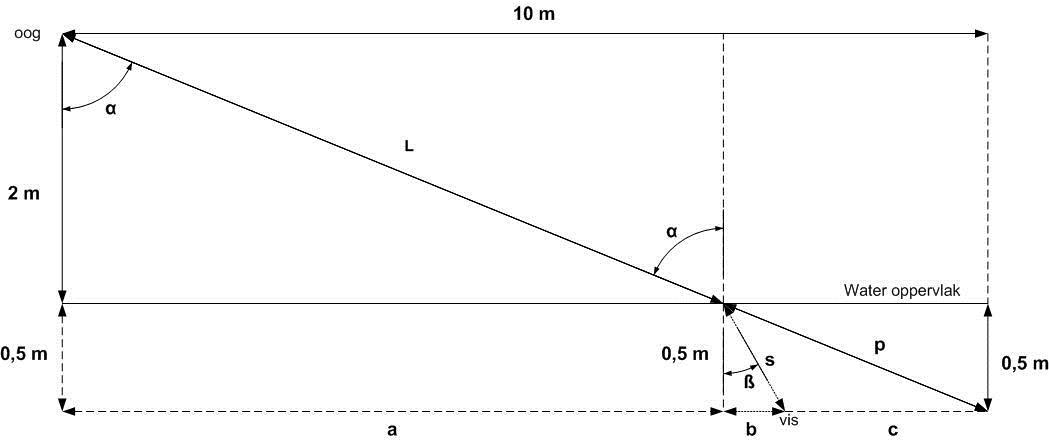
Voorbeeld voor berekening van de werkelijke afstand tot de vis.
Uitgangspunten:
- Ooghoogte 2 meter boven wateroppervlak
- Schijnbare afstand tot de vis 10 meter
- Locatie vis 0,5 meter onder wateroppervlak
- Werkelijke afstand tot de vis (a + b) meter
We zien de vis op het punt waar lijnen p en c elkaar kruisen.
In werkelijkheid bevindt de vis zich daar waar lijnen s en b elkaar kruisen.
Om te weten waar de vis zich bevindt moeten we dus de lengten van de lijnen a en b berekenen. Hierbij wordt enkele keren de welbekende Stelling van Pythagoras toegepast.
| Berekening deelafstand a: |
Berekening deelafstand b: |
| sinus α= (a + b + c)/( l + p) |
sinus α / sinus ß = 1,33 |
| (a + b + c)= 10 |
sinus ß = 0,97 / 1,33 = 0,73 |
| (l + p)2= (2 + 0,5)2 + (10)2 |
sinus ß = b / s = 0,73 |
| (l + p) = 10,3 |
s = b/0,73 |
| Sinus α = 10 / 10,3 = 0,97 |
s2 = 0,52 + b2 |
| Sinus α = a/l =0,97 |
b = 0,5 meter |
| l = a / 0,97 |
|
| l2 = 22 + a2 |
|
| a = 8,1 meter |
|
De werkelijke afstand tot de vis is dus a + b = 8,1 + 0,5 = 8,6 meter.
Door geen rekening te houden met de lichtbreking wordt de vis met 10 - 8,6 = 1,4 meter overworpen.